Defining and Inferring Flows of Information in Neural Circuits

While studying existing methods for inferring information flow in neuroscience, we recognized that Granger Causality does not always capture information flow about a specific message or stimulus. We were able to construct a counterexample wherein Granger Causality inferred the incorrect flow of a message, even when all nodes were observed and when there was no measurement noise. This counterexample also applied to generalizations of Granger Causality, such as Transfer Entropy and Directed Information. We believe that an important reason for the failure of Granger Causality-based tools in this context was the lack of a formal definition for information flow pertaining to a specific message (which could be the stimulus or response in a neuroscientific experiment). The development of such a definition, in turn, was impeded by the absence of a concrete theoretical framework that linked information flow about a message to empirical measurements. We addressed this fundamental gap in our understanding by proposing a new computational model of the brain, and by providing a new definition for information flow about a message within this model.

A central contribution of our work lies in recognizing that tracking the flow of information about a specific message requires that we also account for synergistic flows of information. To understand why, note that a message $M$ may be represented, in combination with some independent “noise” variable $Z$, as $M{+}Z$ and $Z$, across two different brain areas. Represented in this form, if the noise $Z$ is large, it can be very hard to ascertain the presence of information flow about $M$ in the combination $[M{+}Z, Z]$, unless we account for possible synergy between these two brain areas. Accounting for synergy, using conditional mutual information for instance, is thus crucial for tracking information flow in arbitrary computational systems. Relatedly, I have also begun exploring how synergy, along with other partial information measures such as uniqueness and redundancy, arise and interact in neural encoding using entorhinal grid cells as a case study (Venkatesh and Grover, Cosyne, 2020).

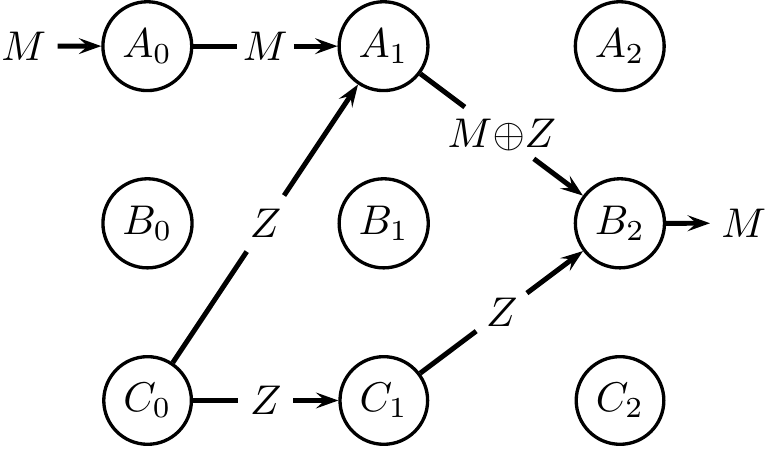
Our new measure of information flow does not have the same pitfalls as Granger Causality, while satisfying our intuition in several canonical examples of computational systems. The full impact of this work continues to be realized, as we explore new measures in greater depth, demonstrate and validate these methods on artificial neural networks, and examine the causal implications of making interventions based on information flow inferences.

 Main paper in Transactions on Info Theory  2015 Granger Causality Counterexample paper  2020 ISIT paper on alternative definitions